Make sure you know your symbols:
< - less than
> - greater than
< - less than or equal to
> - greater than or equal to
To graph an inequality, use an open dot for > and <. Use a closed dot for > and <.
Use the same rules for solving equations to solve an inquality (get the variable by itself by using the inverse operation) - just be sure that you're not using an equals sign (use the inequality symbol instead).
*VERY IMPORTANT*: When multiplying or dividing each side of an inequality by a negative number, reverse the direction of the inequality symbol!!!
Example:
-3x < 12 ---> We need to divide both sides by -3 in order to get x by itself.
-3x < 12
-3 -3
x > -4 ---> Be sure to FLIP the inequality sign!!!
Thursday, November 8, 2012
The Very Mathtastic, Super-Quick Guide to Equations
To solve an equation:
1. Remember, your mission is to get the variable all by itself. .:Cue Mission Impossible theme:.
2. To do this, use the inverse operation. Ask yourself, "What's happening to the variable?" and then
do the opposite of that to both sides. Remember that addition and subtraction are opposites, and
multiplication and division are opposites.
3. Your equation will now tell you what the variable equals.
Examples:
6 + y = 17 ---> What's happening to the variable? We're adding 6 to it. The inverse operation
would be to subtract 6. DON'T FORGET - YOU MUST DO THE SAME
TO BOTH SIDES.
6 + y - 6 = 17 - 6 ---> Solve both sides of the equation.
y = 11
--------------------------------------------------------------------------------------------------------
-2 = a - 10 ---> What's happening to the variable? We're subtracting 10 from it. The inverse
operation would be to add 10.
-2 + 10 = a - 10 + 10 ---> Solve both sides.
8 = a
---------------------------------------------------------------------------------------------------------
3x = -15 ---> Since we're multiplying the variable by 3, the inverse operation would be to divide
by 3.
3x = -15 ---> Remember, the fraction bar means "divided by."
3 3
x = -5
---------------------------------------------------------------------------------------------------------
m = 3 ---> Since we're dividing the variable by 9, the inverse operation would be to multiply by 9.
9
9 x m = 3 x 9 ---> Don't forget, a 9 on top and on bottom cancel each other out.
9
m = 27
--------------------------------------------------------------------------------------------------------
Well, folks, there you have it. Just make sure you:
1. Use the inverse operation
2. Do the same thing to both sides
3. Get the variable by itself
4. Check your answer by plugging that value into the original equation (in place of the variable)
1. Remember, your mission is to get the variable all by itself. .:Cue Mission Impossible theme:.
2. To do this, use the inverse operation. Ask yourself, "What's happening to the variable?" and then
do the opposite of that to both sides. Remember that addition and subtraction are opposites, and
multiplication and division are opposites.
3. Your equation will now tell you what the variable equals.
Examples:
6 + y = 17 ---> What's happening to the variable? We're adding 6 to it. The inverse operation
would be to subtract 6. DON'T FORGET - YOU MUST DO THE SAME
TO BOTH SIDES.
6 + y - 6 = 17 - 6 ---> Solve both sides of the equation.
y = 11
--------------------------------------------------------------------------------------------------------
-2 = a - 10 ---> What's happening to the variable? We're subtracting 10 from it. The inverse
operation would be to add 10.
-2 + 10 = a - 10 + 10 ---> Solve both sides.
8 = a
---------------------------------------------------------------------------------------------------------
3x = -15 ---> Since we're multiplying the variable by 3, the inverse operation would be to divide
by 3.
3x = -15 ---> Remember, the fraction bar means "divided by."
3 3
x = -5
---------------------------------------------------------------------------------------------------------
m = 3 ---> Since we're dividing the variable by 9, the inverse operation would be to multiply by 9.
9
9 x m = 3 x 9 ---> Don't forget, a 9 on top and on bottom cancel each other out.
9
m = 27
--------------------------------------------------------------------------------------------------------
Well, folks, there you have it. Just make sure you:
1. Use the inverse operation
2. Do the same thing to both sides
3. Get the variable by itself
4. Check your answer by plugging that value into the original equation (in place of the variable)
Thursday, October 25, 2012
Assignment 10/25
How would we represent the following inequalities using x as a variable?
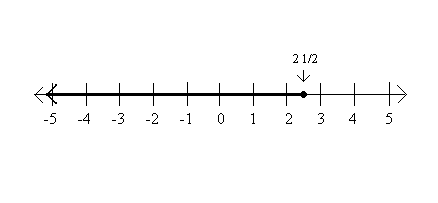
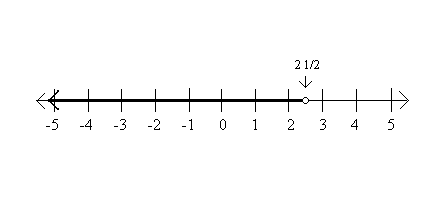

Bonus:

PS - I had fun today having class in the pavilion!!!
Images: Sparknotes.com

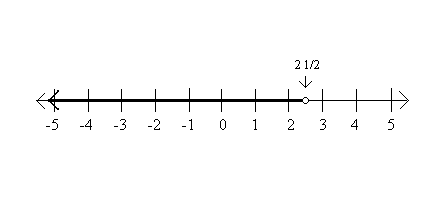

Bonus:

PS - I had fun today having class in the pavilion!!!
Images: Sparknotes.com
Tuesday, October 16, 2012
Extraaaaaa Credit!!!
Simplify the following expression and bring to class tomorrow. A correct answer will earn you 2 pts extra credit.
4x - 5 + 3x + 2y - y
4x - 5 + 3x + 2y - y
Tuesday, October 9, 2012
Properties of Numbers
Here's a summary of the number properties we're discussing @ the beginning of Chp. 2.
Commutative Properties of Addition and Multiplication
Changing the order of the numbers you're adding or multiplying won't change the answer.
Examples:
6 + 4 = 4 + 6
9 x 5 = 5 x 9
a + b = b + a
a x b = b x a
Associative Properties of Addition and Multiplication
If you're only adding numbers or only multiplying numbers (no other operations), changing how the numbers are grouped won't change the anwers.
Examples:
(2 + 7) + 3 = 2 + (7 + 3)
(9 x 4)5 = 9(4 x 5)
(a + b) + c = a + (b + c)
(ab)c = a(bc)
Identity Properties of Addition and Multiplication
Any number plus zero = the original number.
Any number times 1 = the original number.
Examples:
12 + 0 = 12
10 x 1 = 10
a + 0 = a
a x 1 = a
Check back later for pictures that illustrate these properties. Is everyone looking forward to Blacrock?! :)
Commutative Properties of Addition and Multiplication
Changing the order of the numbers you're adding or multiplying won't change the answer.
Examples:
6 + 4 = 4 + 6
9 x 5 = 5 x 9
a + b = b + a
a x b = b x a
Associative Properties of Addition and Multiplication
If you're only adding numbers or only multiplying numbers (no other operations), changing how the numbers are grouped won't change the anwers.
Examples:
(2 + 7) + 3 = 2 + (7 + 3)
(9 x 4)5 = 9(4 x 5)
(a + b) + c = a + (b + c)
(ab)c = a(bc)
Identity Properties of Addition and Multiplication
Any number plus zero = the original number.
Any number times 1 = the original number.
Examples:
12 + 0 = 12
10 x 1 = 10
a + 0 = a
a x 1 = a
Check back later for pictures that illustrate these properties. Is everyone looking forward to Blacrock?! :)
Friday, September 28, 2012
Coordinate Plane Recap + Blog winners
Take a look at this coordinate plane:
 |
| rblewis.net Remember that we find the coordinates of a point by first looking at the value on the x-axis (horizontal), then at the value on the y-axis (vertical).
Example:
To find the coordinates for point A, first locate where it lies on the x-axis (look at the line that goes left to right). It's at positive 4, so our first value for the coordinate is 4.
Then, locate where point A lies on the y-axis (look at the line that goes up and down). This value is also positive 4, so our second value for the coordinate is 4.
Since the format for a point on the coordinate plane is (x, y) - plug the values in. In this case, the coordinate for point A is (4,4).
Here are the other coordinates. Study them to make sure you know how/why these are the correct numbers:
B: (-3, -3)
C: (3, -6)
D: (-5, 2)
Now, for some goodies. I completely forgot to post the winners of our pattern challenge! Check out these great questions:
|
Thursday, September 27, 2012
Assignment 9/27 & What's coming up tomorrow!!!
Read 1-10 in your textbook. The section is about the coordinate plane. Then, watch "The Coordinate Plane" on KhanAcademy: http://www.khanacademy.org/math/algebra/linear-equations-and-inequalitie/v/the-coordinate-plane
Try the first 5 questions in your textbook for 1-10.
As long as it doesn't rain, we will be having class oustide tomorrow - looking forward to some fun stuff with the coordinate plane! :)
Try the first 5 questions in your textbook for 1-10.
As long as it doesn't rain, we will be having class oustide tomorrow - looking forward to some fun stuff with the coordinate plane! :)
Multiplying/Dividing Integers
Rules for multiplying/dividing integers (these should be in your notes):
(Please note that while all these examples include multiplication, the same rules apply to division.)
* When multiplying or dividing, if both numbers have the same sign, the answer is positive. *
Examples:
6 x 5 = 30 ---> Both 6 and 5 have the same sign (they're positive). The answer is positive.
-7 x -3 = -21 ---> Both -7 and -3 have the same sign (they're negative). The answer is positive.
* When multiplying or dividing, if the two numbers have different signs, the answer is negative. *
Example:
-4 x 8 = -32 ---> -4 and 8 have different signs (one is positive, the other negative). The answer is negative.
Some reminders for multiplying or dividing with more than two integers - you have two options:
1. Use order of operations to do one operation at a time. Example (remember that numbers in parentheses with no operations next to each other means multiply!):
-3(2)(-5) ---> Multiply left to right. Start with -3 x 2.
-6(-5) ---> Negative x negative = a positive.
= 30
OR
2. Use the following rule:
When solving multiplication or addition for more than two numbers, an even number of negatives gives a positive answer. An odd number of negatives gives a negative answer.
Examples:
-4(3)(-2)(-1)(-2) ---> I see an even number of negative numbers (4 of them) - positive answer!
= 48
2(-3)(-5)(1)(-4) ---> I see an odd number of negative numbers (3 of them) - negative answer!
= -120
(Please note that while all these examples include multiplication, the same rules apply to division.)
* When multiplying or dividing, if both numbers have the same sign, the answer is positive. *
Examples:
6 x 5 = 30 ---> Both 6 and 5 have the same sign (they're positive). The answer is positive.
-7 x -3 = -21 ---> Both -7 and -3 have the same sign (they're negative). The answer is positive.
* When multiplying or dividing, if the two numbers have different signs, the answer is negative. *
Example:
-4 x 8 = -32 ---> -4 and 8 have different signs (one is positive, the other negative). The answer is negative.
Some reminders for multiplying or dividing with more than two integers - you have two options:
1. Use order of operations to do one operation at a time. Example (remember that numbers in parentheses with no operations next to each other means multiply!):
-3(2)(-5) ---> Multiply left to right. Start with -3 x 2.
-6(-5) ---> Negative x negative = a positive.
= 30
OR
2. Use the following rule:
When solving multiplication or addition for more than two numbers, an even number of negatives gives a positive answer. An odd number of negatives gives a negative answer.
Examples:
-4(3)(-2)(-1)(-2) ---> I see an even number of negative numbers (4 of them) - positive answer!
= 48
2(-3)(-5)(1)(-4) ---> I see an odd number of negative numbers (3 of them) - negative answer!
= -120
Wednesday, September 26, 2012
Some awesometastic integer stuff!
Check out the following videos for integer rules! Do you like rap? Rock? Country? We've got it all:
(Videos courtesy of TeacherTube)
Remember when we talked about how the subtraction problem with integers self-destructs after you turn it into an addition problem (using the KFC method?) Here's L.W.'s rendition... :)
Tee hee! LOVE it!
And finally, last but not least, is a great website that explains WHY when we multiply a negative by a negative, we get a positive. This one's for you, K.P.! - http://www.mathsisfun.com/multiplying-negatives.html
Monday, September 24, 2012
WoRkShOp
Hello to all of my wonderful, brilliant, hard-working Pre-Algebra students!
I know workshop can be pretty intense, but I need to make sure each and every one of you know how to do the problems that were on Friday's quiz correctly. Make sure you have your Math notebook and a pencil out and ready to go if you are in workshop.
Some of the things I'm noticing:
While many of you are able to use the number-line system in your head to solve for the adding of integers, mental math can sometimes be tricky. If you use this method, you can always check your answer by using the abolute value method (see previous post).
Remember that, when using the absolute value method, you must find the difference between the two absolute values - many of you are then adding those absolute values, but you must find the difference.
Example:
3 + (-5)
Absolute values: 3, 5 ---> What's the difference between these numbers? (How many numbers between 3 and 5?)
There is a difference of 2.
Is the 2 negative or positve? 5 is the greatest absolute value - and the original number was -5. Therefore, our answer is negative: -2
Keep practicing the KFC method for subtraction. And remember, once you turn your subtraction problem into addition (adding the opposite), forget the subtraction problem ever existed. Some of you are using the absolute value method for the addition part and then are looking back at the subtraction problem to figure out if your answer is negative or positive. Sometimes it's a good idea to just cross it out - that way you'll remember to just treat the problem exactly like an addition problem:
See you tomorrow for more workshop.
Thursday, September 20, 2012
Just a few reminders...
Open-note quiz tomorrow on 1-4 through 1-8!
The quiz will cover:
Absolute value
Adding/subtracting integers
Inductive reasoning & patterns
Please be sure to have your notes organized & ready for tomorrow. If you're nervous about adding/subtracting with negative numbers, be sure to go back through the blog for step-by-step reminders.
- Positive + Positive = Positive
- Negative + Negative = Negative
- Adding two numbers with different signs: Find absolute values. Determine difference between
absolute values. Use the sign of the number that has the greatest absolute value.
- Change to addition and add the opposite (KEEP, FLIP, CHANGE). *Once you've turned your
subtraction problem to addition, forget about the subtraction part. You are now solving an addition
problem and should proceed with the rules above.
Check back tomorrow for our 3 feature questions from last night's homework!
The quiz will cover:
Absolute value
Adding/subtracting integers
Inductive reasoning & patterns
Please be sure to have your notes organized & ready for tomorrow. If you're nervous about adding/subtracting with negative numbers, be sure to go back through the blog for step-by-step reminders.
- Positive + Positive = Positive
- Negative + Negative = Negative
- Adding two numbers with different signs: Find absolute values. Determine difference between
absolute values. Use the sign of the number that has the greatest absolute value.
- Change to addition and add the opposite (KEEP, FLIP, CHANGE). *Once you've turned your
subtraction problem to addition, forget about the subtraction part. You are now solving an addition
problem and should proceed with the rules above.
Check back tomorrow for our 3 feature questions from last night's homework!
Monday, September 17, 2012
Fried Chicken and... Subtraction?!
*Please read the post below this one for tonight's KhanAcademy assignment*
Scared of subtraction involving negative integers? Don't be - remember, it's just addition in disguise!
The rule for subtraction is:
Add the OpPoSiTe!
Who likes fried chicken? It's one of my all-time favorites. :)

Img: thebittenword.com
So... what does fried chicken have to do with subtracting integers? Check out this cool chart from passyworldofmathematics.com:

Then, solve your problem as an addition problem. Here are a few examples:
-5 - 3 = ?
-5 + (-3) = -8 ---> Both numbers are the same sign, so we can add like normal and keep the sign.
7 - (-2) = ?
7 + 2 = 9 ---> Again, both numbers are the same sign, so we can add like normal and keep the sign.
4 - 8 = ?
4 + (-8) = ? ---> Now we've got addition with two different signs, so remember to use your absolute values!
The absolute values are 4 and 8. The difference between 4 and 8 is 4. Now, is it negative or positive? Look at the original number that had the greatest absolute value: -8. Since it's negative, we know the answer is -4.
If you are self-checking subtraction of integers tonight, here are the answers to the Quick Checks from 1-6 (pgs. 30 & 31):
1) a. -5
b. -1
c. -3
2) a. -4
b. -6
c. 5
3) a. 35
b. -106
c. -46
HaPpY SuBtRaCtInG!
Scared of subtraction involving negative integers? Don't be - remember, it's just addition in disguise!
The rule for subtraction is:
Add the OpPoSiTe!
Who likes fried chicken? It's one of my all-time favorites. :)
Img: thebittenword.com
So... what does fried chicken have to do with subtracting integers? Check out this cool chart from passyworldofmathematics.com:

Then, solve your problem as an addition problem. Here are a few examples:
-5 - 3 = ?
-5 + (-3) = -8 ---> Both numbers are the same sign, so we can add like normal and keep the sign.
7 - (-2) = ?
7 + 2 = 9 ---> Again, both numbers are the same sign, so we can add like normal and keep the sign.
4 - 8 = ?
4 + (-8) = ? ---> Now we've got addition with two different signs, so remember to use your absolute values!
The absolute values are 4 and 8. The difference between 4 and 8 is 4. Now, is it negative or positive? Look at the original number that had the greatest absolute value: -8. Since it's negative, we know the answer is -4.
If you are self-checking subtraction of integers tonight, here are the answers to the Quick Checks from 1-6 (pgs. 30 & 31):
1) a. -5
b. -1
c. -3
2) a. -4
b. -6
c. 5
3) a. 35
b. -106
c. -46
HaPpY SuBtRaCtInG!
Assignment 9/17
Watch the following video on Inductive Patterns:
http://www.khanacademy.org/math/statistics/v/u03-l1-t1-we2-inductive-patterns
OR read 1-7 in your textbook.
*I will be posting the answers to the Quick-Checks for 1-6 as well as tips for subtracting integers in a short while.*
http://www.khanacademy.org/math/statistics/v/u03-l1-t1-we2-inductive-patterns
OR read 1-7 in your textbook.
*I will be posting the answers to the Quick-Checks for 1-6 as well as tips for subtracting integers in a short while.*
Wednesday, September 12, 2012
It's GAME time! :)
Greetings, 6th grade earthlings!
Here is the link to the orbit integers game we played in class today. It's a great game for practicing addition with negative and positive integers. Remember to take your time - the spaceship gets "faster" with more correct answer, not quick answers. Have fun!
http://www.arcademics.com/games/orbit-integers/orbit-integers.html
Here is the link to the orbit integers game we played in class today. It's a great game for practicing addition with negative and positive integers. Remember to take your time - the spaceship gets "faster" with more correct answer, not quick answers. Have fun!
http://www.arcademics.com/games/orbit-integers/orbit-integers.html
Tuesday, September 11, 2012
Adding Integers with Different Signs
(Don't forget - to add integers with the same sign, just add like normal and keep the sign!)
Let's review the 3 methods we can use to add integers with different signs:
1. Use a number line. From your starting point, move to the right if adding a positive integer; move to the left if adding a negative integer.
2. Use the method you have in your notes:
1. Find the absolute values of the two numbers (ignore the negatives).
2. Find the difference between the absolute values.
3. Keep the sign of the number with the greatest absolute value.
Example:
-7 + 4
|-7| + |4|
7 - 4 -----> Notice that after we determined the absolute value, we changed it to subtraction.
= 3 -----> Since the number with the greatest absolute value was -7, the answer becomes negative.
= - 3
3. Use counters/the "Integer Wars" method! Place negative and positive symbols inside a shape of your choosing.
The following picture represents 4 + (-5):
Since 1 positive is cancelled out by one negative, we are left with this, which represents -1:
And voila! You have your answer :) You can also think of it like a battle: There is a negative side and a positive side. Which side has more? The negative side, so we know our answer will be negative. By how many? One more - so we know our answer will be -1.
If you're having a hard time adding integers in your head, any of these 3 methods will help you out. Happy adding!
Let's review the 3 methods we can use to add integers with different signs:
1. Use a number line. From your starting point, move to the right if adding a positive integer; move to the left if adding a negative integer.
2. Use the method you have in your notes:
1. Find the absolute values of the two numbers (ignore the negatives).
2. Find the difference between the absolute values.
3. Keep the sign of the number with the greatest absolute value.
Example:
-7 + 4
|-7| + |4|
7 - 4 -----> Notice that after we determined the absolute value, we changed it to subtraction.
= 3 -----> Since the number with the greatest absolute value was -7, the answer becomes negative.
= - 3
3. Use counters/the "Integer Wars" method! Place negative and positive symbols inside a shape of your choosing.
The following picture represents 4 + (-5):
Since 1 positive is cancelled out by one negative, we are left with this, which represents -1:
And voila! You have your answer :) You can also think of it like a battle: There is a negative side and a positive side. Which side has more? The negative side, so we know our answer will be negative. By how many? One more - so we know our answer will be -1.
If you're having a hard time adding integers in your head, any of these 3 methods will help you out. Happy adding!
Friday, September 7, 2012
Number Line Fun
We had a little fun outside today with a number line :) We talked about how negative integers, even though they seem to increase as you go to the left, actually decrease in value. We then explored opposites and found that -3 and 3 (opposite integers) are the same distance from zero. Everyone did a fantastic job with our human addition game using both positive and negative integers! Keep up the good work!
Thursday, September 6, 2012
Assignment 3 - Weekend of 9/7
Are we having fun with number lines yet? :)
Remember from today's activity that a number line is set up like this, with negative numbers to the left of zero, and positive numbers to the right:
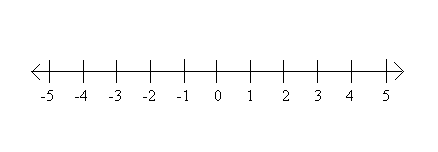
*Note that the negative numbers seem to increase as you go left, but remember that the further left you go, the value decreases. Kind of like if you were representing negative points in a game show; a team with -7 points has LESS points than a team with -3.*
Assignment Part 1:
1. Go to PHSchool.com
2. Under "Web Codes," enter the code ade-0104.
3. Watch the two videos under "English" - Representing situations with integers and Finding absolute values.
Assignment Part 2:
Click the link to watch a video on Absolute Value from Khan Academy:
http://www.khanacademy.org/math/algebra/absolute-value/v/absolute-value-and-number-lines
OR type "Absolute Value and Number Lines" into the search box and select the video.
Remember from today's activity that a number line is set up like this, with negative numbers to the left of zero, and positive numbers to the right:
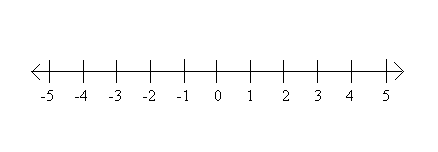
*Note that the negative numbers seem to increase as you go left, but remember that the further left you go, the value decreases. Kind of like if you were representing negative points in a game show; a team with -7 points has LESS points than a team with -3.*
Assignment Part 1:
1. Go to PHSchool.com
2. Under "Web Codes," enter the code ade-0104.
3. Watch the two videos under "English" - Representing situations with integers and Finding absolute values.
Assignment Part 2:
Click the link to watch a video on Absolute Value from Khan Academy:
http://www.khanacademy.org/math/algebra/absolute-value/v/absolute-value-and-number-lines
OR type "Absolute Value and Number Lines" into the search box and select the video.
Tuesday, September 4, 2012
Assignment 2 - Homework for Wed., 9/5
Watch the video "Variables Expressions & Equations" on Khan Academy.
The video will be a review of what we discussed in class today.
Don't worry about the negative numbers, exponents, and square roots information he brings up towards the end of the video. We'll get to that stuff later. :)
Link: http://www.khanacademy.org/math/algebra/solving-linear-equations-and-inequalities/v/variables-expressions-and-equations
The video will be a review of what we discussed in class today.
Don't worry about the negative numbers, exponents, and square roots information he brings up towards the end of the video. We'll get to that stuff later. :)
Link: http://www.khanacademy.org/math/algebra/solving-linear-equations-and-inequalities/v/variables-expressions-and-equations
Tuesday, August 28, 2012
Assignment 1
Hello all! Welcome to your very first assignment :)
1. Sign into your Khan Academy account.
2. Click the link below to watch your first video. If it does not take you to a video called "Introduction to Order of Operations," go to the search box at the top of the website and type "Introduction to Order of Operations" - then, select the video.
http://www.khanacademy.org/math/arithmetic/order-of-operations/v/introduction-to-order-of-operations
3. After the video, click the gray "Practice" button that appears on the screen. Try to earn as many energy points as you can! Please remember what we talked about in class: PLEASE EXCUSE MY DEAR AUNT SALLY. Remember that the numerator and denominator in a fraction are grouped together (as though they had parentheses).
*If your practice questions give you negative integers and you're not sure how to add/subtract them, just try your best.*
1. Sign into your Khan Academy account.
2. Click the link below to watch your first video. If it does not take you to a video called "Introduction to Order of Operations," go to the search box at the top of the website and type "Introduction to Order of Operations" - then, select the video.
http://www.khanacademy.org/math/arithmetic/order-of-operations/v/introduction-to-order-of-operations
3. After the video, click the gray "Practice" button that appears on the screen. Try to earn as many energy points as you can! Please remember what we talked about in class: PLEASE EXCUSE MY DEAR AUNT SALLY. Remember that the numerator and denominator in a fraction are grouped together (as though they had parentheses).
*If your practice questions give you negative integers and you're not sure how to add/subtract them, just try your best.*
Subscribe to:
Comments (Atom)












