Assignment 10/25

How would we represent the following inequalities using x as a variable?




Bonus:


PS - I had fun today having class in the pavilion!!!

Images: Sparknotes.com

Extraaaaaa Credit!!!

Simplify the following expression and bring to class tomorrow. A correct answer will earn you 2 pts extra credit.

4x - 5 + 3x + 2y - y

HuMaN MaTh - Properties

Commutative Property

 

 

Associative Property

 

 

Identity Property

 

 

 

Properties of Numbers

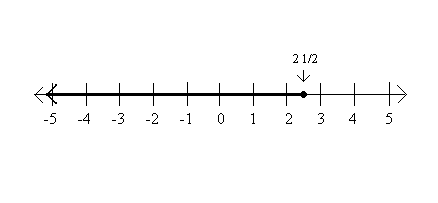
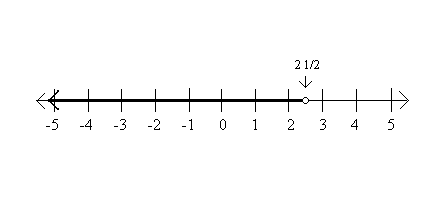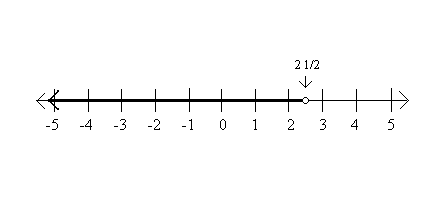Here's a summary of the number properties we're discussing @ the beginning of Chp. 2.


Commutative Properties of Addition and Multiplication
Changing the order of the numbers you're adding or multiplying won't change the answer.
Examples:
6 + 4 = 4 + 6
9 x 5 = 5 x 9
a + b = b + a
a x b = b x a

Associative Properties of Addition and Multiplication
If you're only adding numbers or only multiplying numbers (no other operations), changing how the numbers are grouped won't change the anwers.
Examples:
(2 + 7) + 3 = 2 + (7 + 3)
(9 x 4)5 = 9(4 x 5)
(a + b) + c = a + (b + c)
(ab)c = a(bc)

Identity Properties of Addition and Multiplication
Any number plus zero = the original number.
Any number times 1 = the original number.
Examples:
12 + 0 = 12
10 x 1 = 10
a + 0 = a
a x 1 = a


Check back later for pictures that illustrate these properties. Is everyone looking forward to Blacrock?! :)